Sortering er en grunnleggende operasjon der elementene i en matrise er arrangert i en bestemt rekkefølge for å forbedre søkbarheten. I enkle ord blir dataene sortert slik at det enkelt kan søges.
Sammenligningstabel
| Grunnlag for sammenligning | Innsettings sortering | Valg Sorter |
|---|---|---|
| grunn~~POS=TRUNC | Dataene sorteres ved å sette inn dataene i en eksisterende sortert fil. | Dataene sorteres ved å velge og plassere de påfølgende elementene på sortert sted. |
| Natur | Stabil | Ustabil |
| Prosess som skal følges | Elementer er kjent på forhånd mens plassering for å plassere dem søkte. | Plassering er tidligere kjent mens elementene søktes. |
| Umiddelbare data | Innsats sortering er live sortering teknikk som kan håndtere umiddelbare data. | Det kan ikke håndtere umiddelbare data, det må være til stede i begynnelsen. |
| Beste tilfelle kompleksitet | På) | O (n 2 ) |
Definisjon av Insertion Sorter
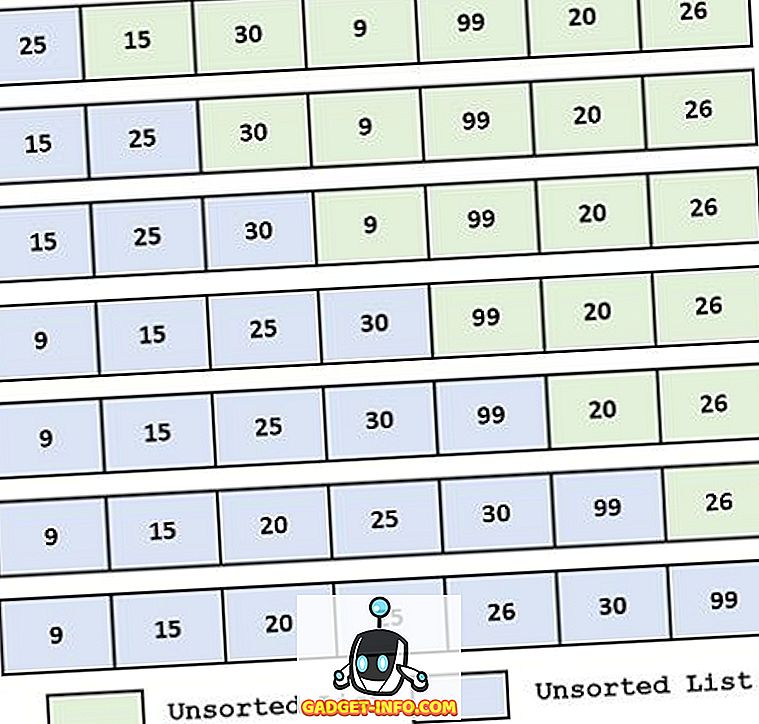
Innførings sortering fungerer ved å sette inn settet av verdier i den eksisterende sorterte filen. Den konstruerer den sorterte oppsettet ved å sette inn et enkelt element om gangen. Denne prosessen fortsetter til hele arrayet er sortert i noen rekkefølge. Det primære konseptet bak innsettingstypen er å sette hvert element inn på sitt passende sted i den endelige listen. Innleggingsmetoden sparer en effektiv mengde minne.
Arbeide med innsettings sorteringen
- Den bruker to sett med arrayer hvor man lagrer de sorterte dataene og andre på usorterte data.
- Sorteringsalgoritmen virker til det finnes elementer i usorterte settet.
- La oss anta at det er 'n' tallelementer i matrisen. I utgangspunktet finnes elementet med indeks 0 (LB = 0) i det sorterte settet. Resterende elementer er i den usorterte partisjonen på listen.
- Det første elementet i den usorterte delen har arrayindeks 1 (Hvis LB = 0).
- Etter hver iterasjon velger den det første elementet i den usorterte partisjonen og setter den inn på riktig sted i det sorterte settet.
Fordeler med Insertion sort
- Enkel implementert og svært effektiv når den brukes med små datamengder.
- Det ekstra minnekortbehovet for innføringssort er mindre (dvs. O (1)).
- Det anses å være levende sorteringsteknikk, da listen kan sorteres etter hvert som de nye elementene mottas.
- Det er raskere enn andre sorteringsalgoritmer.
Eksempel:
Definisjon av utvalgssortering
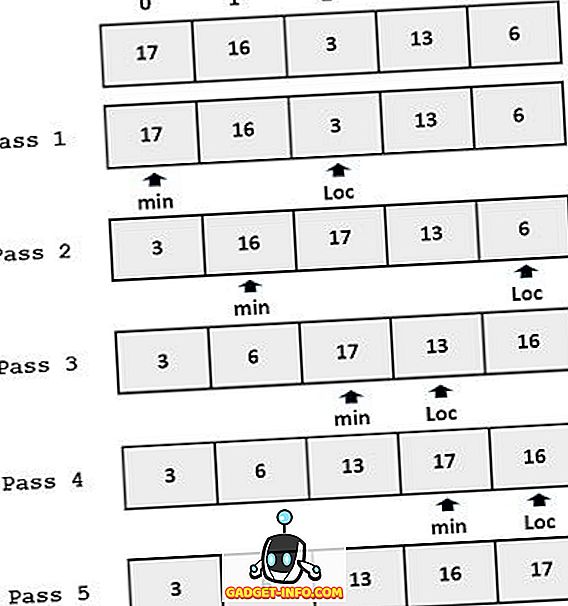
Sorteringsvalget utfører sortering ved å søke etter minimumsverdienummeret og plassere det i første eller siste posisjon i henhold til ordren (stigende eller synkende). Prosessen med å søke minimumsnøkkelen og plassere den i riktig posisjon, fortsetter til alle elementene er plassert i riktig posisjon.
Arbeide med utvalgssorteringen
- Anta en array ARR med N elementer i minnet.
- I det første passet søkes den minste nøkkelen sammen med sin posisjon, da ARR [POS] byttes med ARR [0]. Derfor er ARR [0] sortert.
- I det andre passet bestemmes posisjonen av den minste verdien i underarrayet av N-1-elementene. Bytt ARR [POS] med ARR [1].
- I pass N-1 utføres samme prosess for å sortere N-tallet av elementer.
Eksempel:
Nøkkelforskjeller mellom sorteringsvalg og utvalgssortering
- Innsatsen sorterer vanligvis utfører innsatsoperasjonen. Tvert imot utfører sorterings sorter utvalget og plasseringen av de nødvendige elementene.
- Innsats sortering sies å være stabil, mens utvalgssort er ikke en stabil algoritme.
- I innføringssortalgoritmen er elementene tidligere kjent. I kontrast inneholder sorterings sorteringen plasseringen på forhånd.
- Innsats sortering er en levende sorteringsteknikk hvor de ankomne elementene umiddelbart sorteres i listen, mens utvalgssort kan ikke fungere bra med umiddelbare data.
- Innsats sorteringen har O (n) kjøretid i beste tilfelle. I motsetning til det beste tilfelle kjører tiden kompleksiteten til utvalgssort er O (n2).
Kompleksitet av innsettings sortering
Den beste saken kompleksiteten av innførings sorteringen er O (n) ganger, det vil si når arrayet tidligere er sortert. På samme måte, når arrayet er sortert i omvendt rekkefølge, skal det første elementet i det usorterte arrayet sammenlignes med hvert element i det sorterte settet. Så, i verste fall, kjører tiden for Insertion sorter er kvadratisk, dvs. O (n2) . I gjennomsnitt må det også være minimum (k-1) / 2 sammenligninger. Derfor har gjennomsnittlig sak også kvadratisk kjøretid O (n2).
Kompleksiteten til utvalgssorteringen
Som arbeidet med utvelgelse er sorteringen ikke avhengig av den opprinnelige rekkefølgen av elementene i matrisen, så det er ikke mye forskjell mellom beste tilfelle og verste fall kompleksiteten til utvalgssort.
Valget sorterer velger minimumsverdien, i valgprosessen blir alle 'n' antall elementer skannet; Derfor blir n-1 sammenligninger gjort i første pass. Da blir elementene byttet ut. På samme måte i det andre passet også for å finne det nest minste elementet, krever vi skanning av hvile n-1 elementer, og prosessen fortsetter til hele sorteringen sorteres.
Dermed er kjøretidskompleksiteten til utvalgssortet O (n2) .
= (n-1) + (n-2) + ......... .. + 2 + 1
= n (n-1) / 2 = 0 (n2)
Konklusjon
Blant begge sorteringsalgoritmen er innføringssorten rask, effektiv og stabil, mens utvalgssort bare virker effektivt når det lille settet av elementer er involvert eller listen er delvis tidligere sortert. Antall sammenligninger som er gjort ved å velge sortering, er større enn bevegelsene som utføres, mens i innsetting sorteres antall ganger et element flyttes eller byttes, er større enn sammenligningene som er gjort.