I motsetning til standardavvik er kvadratroten av den numeriske verdien oppnådd under beregning av variansen. Mange kontrasterer disse to matematiske konseptene. Så, denne artikkelen gjør et forsøk på å kaste lys på den viktige forskjellen mellom varians og standardavvik.
Sammenligningstabel
| Grunnlag for sammenligning | varians | Standardavvik |
|---|---|---|
| Betydning | Varians er en numerisk verdi som beskriver variabiliteten av observasjoner fra dens aritmetiske gjennomsnitt. | Standardavvik er et mål for spredning av observasjoner i et datasett. |
| Hva er det? | Det er gjennomsnittet av kvadratiske avvik. | Det er rotenes gjennomsnittlige firkantavvik. |
| Merket som | Sigma-kvadratet (σ ^ 2) | Sigma (σ) |
| Uttrykt i | Kvadratiske enheter | Samme enheter som verdiene i datasettet. |
| indikerer | Hvor langt individer i en gruppe er spredt ut. | Hvor mye observasjoner av et datasett er forskjellig fra dets gjennomsnitt. |
Definisjon av variasjon
I statistikk defineres varians som måling av variabilitet som representerer hvor langt medlemmene i en gruppe er spredt ut. Det finner ut den gjennomsnittlige graden som hver observasjon varierer fra gjennomsnittet. Når variansen av et datasett er liten, viser det datapunktenees nærhet til gjennomsnittet, mens en større variansverdier representerer at observasjonene er svært spredt rundt det aritmetiske middel og fra hverandre.
For uklassifiserte data :
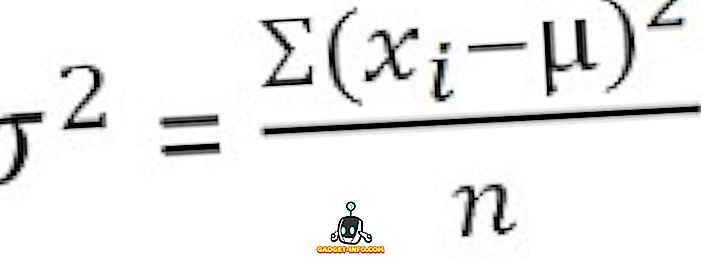
For gruppert frekvensfordeling :
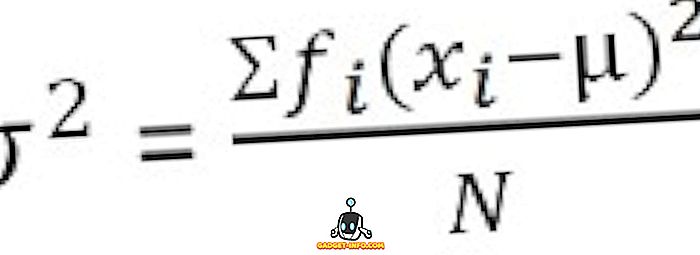
Definisjon av standardavvik
Standardavvik er et mål som kvantifiserer mengden av spredning av observasjonene i et datasett. Den lave standardavviket er en indikator på at scoreene er nært til det aritmetiske gjennomsnittet og en høy standardavvik representerer; Resultatene er spredt over et høyere verdierivå.
For uklassifiserte data :

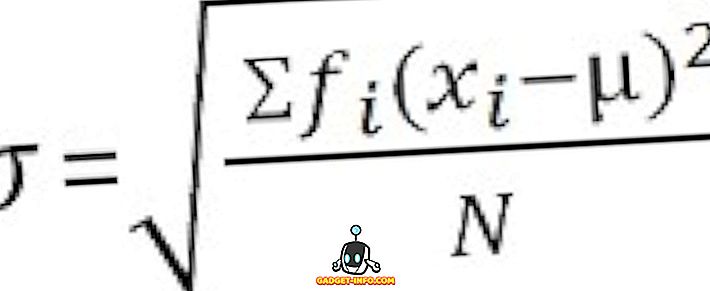
Viktige forskjeller mellom variasjon og standardavvik
Forskjellen mellom standardavvik og varians kan trekkes tydelig av følgende grunner:
- Varians er en numerisk verdi som beskriver variabiliteten av observasjoner fra dens aritmetiske gjennomsnitt. Standardavvik er et mål for spredning av observasjoner i et datasett.
- Variansen er ingenting annet enn et gjennomsnitt av kvadratiske avvik. På den annen side er standardavviket rotenes gjennomsnittlige kvadratfeil.
- Variansen er betegnet med sigma-kvadrat (σ2), mens standardavviket er merket som sigma (σ).
- Variansen uttrykkes i kvadratiske enheter som vanligvis er større enn verdiene i det oppgitte datasettet. I motsetning til standardavvik som uttrykkes i de samme enhetene som verdiene i datasettet.
- Variansen måler hvor langt personer i en gruppe er spredt ut. Omvendt måler Standard Deviation hvor mye observasjoner av et datasett som er forskjellig fra dets gjennomsnitt.
Illustrasjon
Karakterer skåret av en student i fem fag er henholdsvis 60, 75, 46, 58 og 80. Du må finne ut av standardavviket og variansen.
Først av alt, må du finne ut de gjennomsnittlige,

Så gjennomsnittlig (gjennomsnittlig) karakter er 63, 8
Beregn nå variansen
| X | EN | (Xa) | (XA) ^ 2 |
|---|---|---|---|
| 60 | 63.8 | -3, 8 | 14.44 |
| 75 | 63.8 | 11.2 | 125, 44 |
| 46 | 63.8 | -17, 8 | 316, 84 |
| 58 | 63.8 | 5.8 | 33.64 |
| 80 | 63.8 | 16.2 | 262, 44 |
Hvor, X = Observasjoner
A = Aritmetisk middel
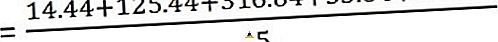
Og standardavvik er -

likheter
- Både varians og standardavvik er alltid positive.
- Hvis alle observasjonene i et datasett er identiske, vil standardavviket og variansen være null.
Konklusjon
Disse to er grunnleggende statistiske termer, som spiller en viktig rolle i ulike sektorer. Standardavviket foretrekkes over gjennomsnittet som det uttrykkes i de samme enhetene som målingene, mens variansen uttrykkes i enhetene som er større enn det gitte datasettet.