I motsetning til dette, i tilfelle av en kombinasjon, har bestillingen ingen betydning i det hele tatt. Ikke bare i matematikk, men også i praktisk liv, går vi gjennom disse to konseptene regelmessig. Selv om vi ikke merker det. Så ta en lese av artikkelen nøye, for å vite hvordan disse to konseptene er forskjellige.
Sammenligningstabel
| Grunnlag for sammenligning | permutasjon | Kombinasjon |
|---|---|---|
| Betydning | Permutasjon refererer til de forskjellige måtene å ordne et sett med objekter i en sekvensiell rekkefølge. | Kombinasjon refererer til flere måter å velge elementer fra et stort sett med objekter, slik at bestillingen deres ikke betyr noe. |
| Rekkefølge | Aktuell | Irrelevant |
| betegner | Ordning | utvalg |
| Hva er det? | Bestilte elementer | Uordnede sett |
| svar | Hvor mange forskjellige arrangement kan opprettes fra et gitt sett med objekter? | Hvor mange forskjellige grupper kan velges fra en større gruppe objekter? |
| derivasjon | Flere permutasjon fra en enkelt kombinasjon. | Enkel kombinasjon fra en enkelt permutasjon. |
Definisjon av Permutasjon
Vi definerer permutasjon som forskjellige måter å arrangere noen eller alle medlemmer av et sett på i en bestemt rekkefølge. Det innebærer alt mulig arrangement eller omplassering av det angitte settet, i skillebar rekkefølge.
For eksempel, All mulig permutasjon opprettet med bokstaver x, y, z -
- Ved å ta alle tre om gangen er xyz, xzy, yxz, yzx, zxy, zyx.
- Ved å ta to om gangen er xy, xz, yx, yz, zx, zy.
Totalt antall mulige permutasjoner av n ting, tatt r om gangen, kan beregnes som:
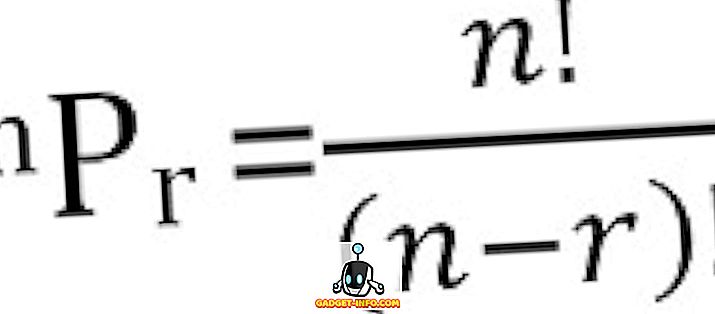
Definisjon av kombinasjon
Kombinasjonen er definert som de forskjellige måtene ved å velge en gruppe ved å ta noen eller alle medlemmer av et sett uten følgende ordre.
For eksempel, Alle mulige kombinasjoner valgt med bokstav m, n, o -
- Når tre av tre bokstaver skal velges, er den eneste kombinasjonen mno
- Når to av tre bokstaver skal velges, er de mulige kombinasjonene mn, nei, om.
Totalt antall mulige kombinasjoner av n ting, tatt r om gangen, kan beregnes som:
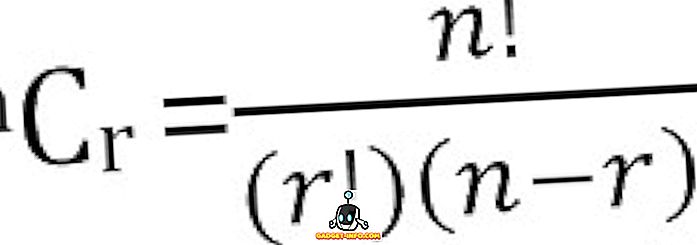
Viktige forskjeller mellom permutasjon og kombinasjon
Forskjellene mellom permutasjon og kombinasjon er trukket tydelig av følgende grunner:
- Begrepet permutasjon refererer til flere måter å arrangere et sett med objekter i en sekvensiell rekkefølge. Kombinasjon innebærer flere måter å velge elementer fra et stort basseng av objekter, slik at bestillingen deres er irrelevant.
- Det primære skillespunktet mellom disse to matematiske begrepene er ordre, plassering og posisjon, dvs. i permutasjonsegenskaper nevnt ovenfor, betyr noe, noe som ikke betyr noe i tilfelle kombinasjonen.
- Permutasjon angir flere måter å ordne ting, personer, tall, alfabeter, farger osv. På den annen side angir kombinasjonen forskjellige måter å velge menyelementer, mat, klær, emner osv.
- Den permutasjon er ingenting annet enn en bestilt kombinasjon, mens kombinasjon innebærer uordnede sett eller sammenkobling av verdier innenfor spesifikke kriterier.
- Mange permutasjoner kan utledes fra en enkelt kombinasjon. Omvendt kan bare en enkelt kombinasjon oppnås fra en enkelt permutasjon.
- Permutasjonssvar Hvor mange forskjellige arrangementer kan opprettes fra et gitt sett med objekter? I motsetning til kombinasjonen som forklarer Hvor mange forskjellige grupper kan plukkes fra en større gruppe objekter?
Eksempel
Anta at det er en situasjon der du må finne ut det totale antall mulige prøver av to av tre objekter A, B, C. I dette spørsmålet må du først forstå, om spørsmålet er relatert til permutasjon eller kombinasjon, og den eneste måten å finne ut dette er å kontrollere om bestillingen er viktig eller ikke.
Hvis bestillingen er signifikant, er spørsmålet relatert til permutasjon, og mulige prøver vil være, AB, BA, BC, CB, AC, CA. Hvor, AB er forskjellig fra BA, er BC forskjellig fra CB og AC er forskjellig CA.
Hvis bestillingen er irrelevant, er spørsmålet relatert til kombinasjonen, og de mulige prøvene vil være AB, BC og CA.
Konklusjon
Med ovennevnte diskusjon er det klart at permutasjon og kombinasjon er forskjellige termer, som brukes i matematikk, statistikk, forskning og vårt daglige liv. Et poeng å huske, om disse to konseptene er at for et gitt sett med objekter vil permutasjon alltid være høyere enn kombinasjonen.