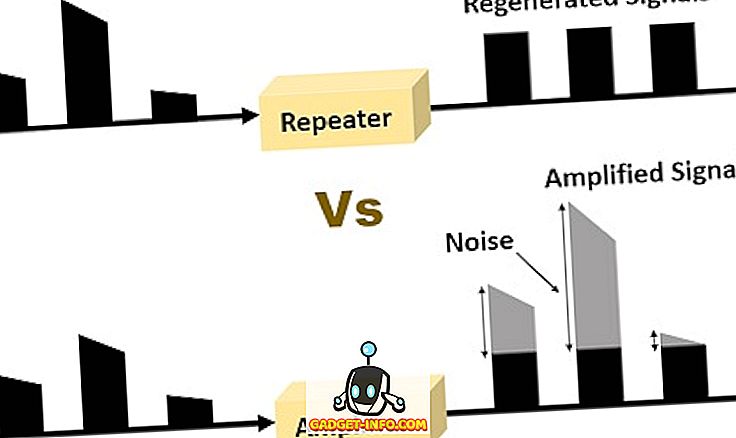
Standard Feil brukes til å måle den statistiske nøyaktigheten av et estimat. Det brukes primært i prosessen med å teste hypotesen og estimeringsintervallet.
Dette er to viktige begreper statistikk, som er mye brukt innen forskning. Forskjellen mellom standardavvik og standardfeil er basert på forskjellen mellom beskrivelsen av data og dens inngang.
Sammenligningstabel
| Grunnlag for sammenligning | Standardavvik | Standard feil |
|---|---|---|
| Betydning | Standardavvik innebærer et mål for spredning av settet av verdier fra deres gjennomsnitt. | Standard Feil connotes måling av statistisk nøyaktighet av et estimat. |
| statistikk | beskrivende | slutnings |
| målinger | Hvor mange observasjoner varierer fra hverandre. | Hvor nøyaktig prøven betyr for den sanne befolkningens gjennomsnitt. |
| Fordeling | Distribusjon av observasjon angående normal kurve. | Fordeling av et estimat for normal kurve. |
| Formel | Kvadratroten av variansen | Standardavvik divideres med kvadratrot av prøvestørrelse. |
| Økning i utvalgsstørrelse | Gir et mer spesifikt mål for standardavvik. | Senker standard feil. |
Definisjon av standardavvik
Standardavvik, er et mål for spredningen av en serie eller avstanden fra standarden. I 1893 oppfattet Karl Pearson begrepet standardavvik, noe som utvilsomt er mest brukt i forskning.
Det er kvadratroten av gjennomsnittet av firkanter av avvik fra deres gjennomsnitt. Med andre ord, for et gitt datasett, er standardavviket rot-mean-square-avviket, fra aritmetisk gjennomsnitt. For hele befolkningen er det angitt med gresk bokstav 'sigma (σ)', og for en prøve er det representert av latinske brev 's'.
Standardavvik er et mål som kvantifiserer graden av spredning av settet av observasjoner. Jo lenger datapunkter fra middelverdien, desto større er avviket i datasettet, som representerer at datapunkter er spredt over et bredere spekter av verdier og omvendt.
- For uklassifiserte data:

- For gruppert frekvensfordeling:

Definisjon av standard feil
Du har kanskje observert at forskjellige prøver, med samme størrelse, trukket fra samme befolkning, vil gi ulike verdier av statistikk under vurdering, dvs. prøvemiddel. Standard Feil (SE) angir standardavviket i forskjellige verdier av prøvens gjennomsnitt. Det brukes til å gjøre en sammenligning mellom prøveinnretninger over befolkningene.
Kort sagt er standardfeilen i en statistikk ikke noe annet enn standardavviket i samplingsfordelingen. Det har en stor rolle å spille testen av statistisk hypotese og intervallestimering. Det gir en ide om estimatets nøyaktighet og pålitelighet. Jo mindre standardfeilen er, desto større er enhetligheten i den teoretiske fordeling og omvendt.
- Formel : Standard Feil for sample mean = σ / √n
Hvor, σ er populasjonsstandardavvik
Viktige forskjeller mellom standardavvik og standardfeil
Poengene som er angitt nedenfor er betydelige så langt som forskjellen mellom standardavviket angår:
- Standardavvik er målet som vurderer mengden av variasjon i settet av observasjoner. Standard Feil måler nøyaktigheten av et estimat, det vil si det er målet for variabilitet av den teoretiske fordelingen av en statistikk.
- Standardavvik er en beskrivende statistikk, mens standardfeilen er en inferensiell statistikk.
- Standardavvik måler hvor langt de enkelte verdiene er fra middelverdien. Tvert imot, hvor nær prøven er gjennomsnittlig, er populasjonsmiddelet.
- Standardavvik er fordeling av observasjoner med referanse til normal kurve. I motsetning til dette er standardfeilen fordelingen av et estimat med referanse til normalkurven.
- Standardavvik defineres som kvadratroten av variansen. Omvendt er standardfeilen beskrevet som standardavviket dividert med kvadratroten av prøvestørrelsen.
- Når prøvestørrelsen er hevet, gir den et mer bestemt mål for standardavviket. I motsetning til standardfeil når prøvestørrelsen økes, har standardfeilen en tendens til å synke.
Konklusjon
I stor grad betraktes standardavviket som en av de beste målene for spredning, som måler spredningen av verdier fra den sentrale verdien. På den annen side er standardfeilen hovedsakelig brukt for å sjekke estimatets pålitelighet og nøyaktighet, og jo mindre feilen er, desto større er dens pålitelighet og nøyaktighet.